
Centers of a Triangle
by
Susan Sexton
Prove that the three
perpendicular bisectors of a triangle are concurrent.
Start with triangle RST.
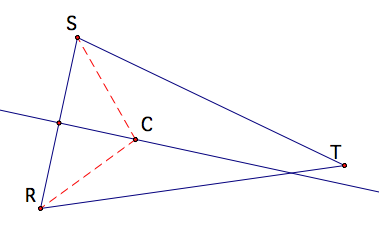
The perpendicular bisector
of segment RS is the set of all points that are the same distant (equidistant)
from both R and S. Therefore any
point that lies on the perpendicular bisector, for instance, point C, will
result in SC=RC.
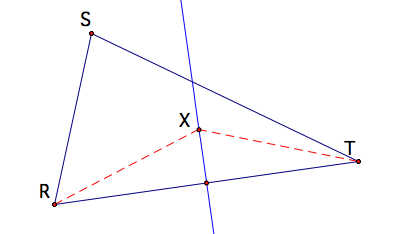
Similarly, the perpendicular bisector of segment RT will be all the points equidistant from R and T. Therefore if X lies on the perpendicular bisector of RT then RX = XT.
So considering segment RS
and segment RT and their respective perpendicular bisectors then the
intersection of the two perpendicular bisectors will result in the point that
is equidistant from R and S and R and T.
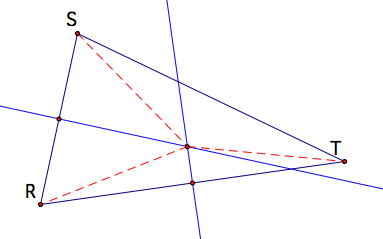
Therefore, using C as the point of intersection, we have RC = SC an RC = TC. So by transitivity we have SC = TC. Since C is equidistant from S and T then C lies on the perpendicular bisector of segment ST. Therefore C is the point of concurrency between the three perpendicular bisectors.
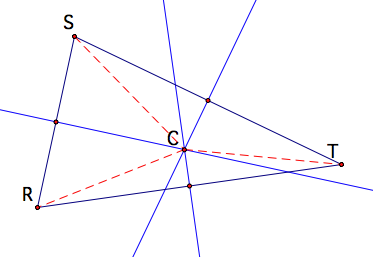
The perpendicular
bisectors of a triangle are also the altitudes of another triangle.
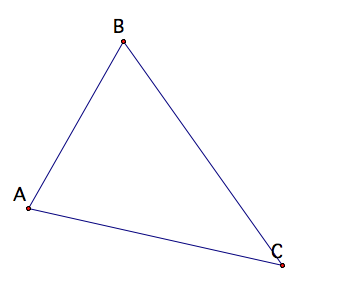
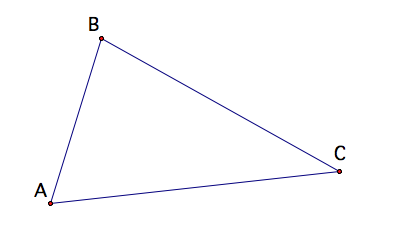
Consider triangle
ABC. I will find another triangle
for which triangle ABC is the medial triangle.
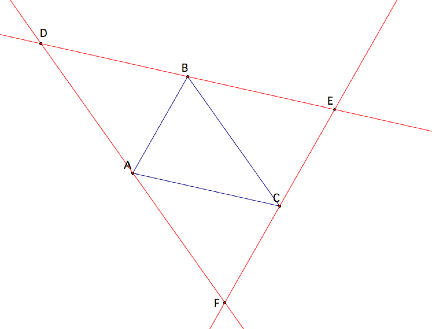
Start with finding the line parallel to each segment of the triangle through the vertex opposite to the segment. For example, find the line parallel to segment AB and passing through vertex C. This will result in a new triangle DEF whose medial triangle is ABC.
By finding the perpendicular bisectors of triangle DEF, these will also be the altitudes of triangle ABC. Since the perpendicular bisectors are concurrent then the altitudes of triangle ABC will also be concurrent at the same point.
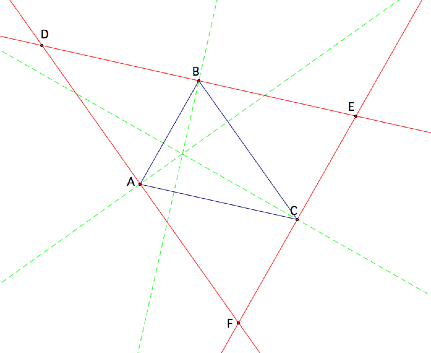
Therefore the altitudes of a triangle are concurrent.
I will prove that the altitudes of a triangle are concurrent using another method . . . one involving circles. Again, consider triangle ABC.
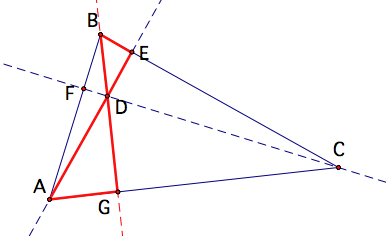
Strategy . . .
Given altitudes CF and AE
that intersect at point D, I will show that the line through BD is
perpendicular to segment AC implying that angle DGA is a right angle.
I will do this by proving that triangles AGD and BED are similar. Angles BDE and ADG are vertical angles and so are of equal measure. So I am half-way to proving the triangles are similar. I only need to prove angles DAG and DBE are of equal measure. This will prove that the triangles are similar and will result in angle BED = angle AGD. Since angle BED is a right angle because of altitude AE then angle AGD will also be a right angle.
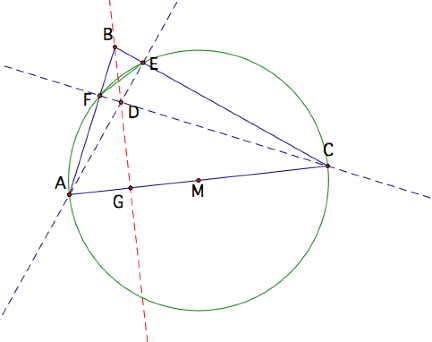
As stated above AE is an
altitude so angles AEB and AEC are right angles. This means that triangle AEC is a right triangle with
hypotenuse AC. There exists a
circle whose diameter is AC and point E on the circle. (This can be proved using the Angle Arc
Theorem.)
To find this circle, I will find the midpoint of AC, point M, and construct a circle of radius MC. Also I will construct segment FE. This will create two angles, angle EFC and angle EAC, that both subtend the same arc, arc EC. Therefore, by the Arc Angle Theorem, angle EFC = angle EAC.
Again, using the same idea
as above, since angle FEB is a right angle then triangle BED is a right
triangle with hypotenuse BD. So
there exists a circle whose diameter is BD and point E on the circle. Use the same process as earlier to find
this circle. So with segment EF,
then angle EFD and angle EBD both subtend arc ED.
Therefore angle EBD = angle EFD.
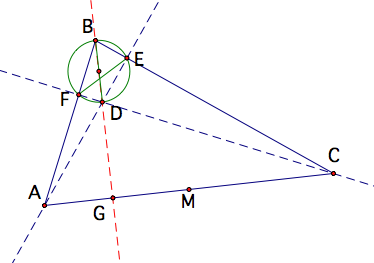
Since angle EFC is the
same as angle EFD then angle EBD = angle EAC. Since angle EAC is the same as angle DAG then angle EBD =
angle DAG. Again since angle BDE =
angle ADG (since they are vertical angles) then triangles AGD and BED are
similar by AA similarity.
Therefore angle DGA is a right angle and so BG is perpendicular to
AC. Thus BG is an altitude of
triangle ABC and the altitudes are concurrent.
There are some ideas
inherent in the proofs that were not discussed here. These include the Arc Angle Theorem and why the circumcenter
of a triangle is the orthocenter of its medial triangle. These would be neat ideas to explore
and prove!
Here are some GSP files to move around and perhaps explore some more.